압력과 부력
유체정역학(Hydrostatics)은 정지하여 있는 유체의 압력이나 힘을 연구하는 학문입니다. 제 블로그에서 다루어질 유체정역학은 대부분 선박에 작용하는 유체의 압력과 힘을 다루게 될 것입니다.
1 압력(Pressure)
압력은 기압, 공압, 수압, 유압 등 종류가 다양하며 대부분 실생활에서 자주 들어보셨을 것입니다. 그 중 물의 무게로 인한 압력인 수압은 조선 공학(naval architect)에서 가장 중요한 압력입니다. 수압은 물에 잠긴 면적에 수직하게 작용하며, 수심이 깊어질수록 증가합니다.
\[ \begin{aligned} P &= \frac{F}{A} \\ &= \frac{\rho g V}{A} \left( = \frac{w V}{A} = \frac{m g}{A} \right) \\ &= \frac{\rho g (h \cdot A)}{A} \\ &= \rho g h \\ \end{aligned} \]
- 압력(\(P\))
- 면적에 작용하는 힘, \([\mathrm{Pa}]\)
- 힘(\(F\))
- 물의 무게, \([\mathrm{N}]\)
- 면적(\(A\))
- 힘이 가해지는 면적, \([\mathrm{m^2}]\)
- 밀도(\(\rho\))
- 단위 부피 당 물의 질량, \([\mathrm{kg/m^3}]\)
- 중력 가속도(\(g\))
- 지구의 중력 가속도, \([\mathrm{m/s^2}]\)
- 부피(\(V\))
- 면적 위부터 수면까지의 물의 부피, \([\mathrm{m^3}]\)
- 수심(\(h\))
- 면적부터 수면까지의 길이, \([\mathrm{m}]\)
- 중량(\(w\))
- 단위 부피당 무게, \([\mathrm{N/m^3}]\)
밀도는 온도에 따라 달라지며 소금물 같은 경우에는 소금의 농도 또한 밀도에 영향을 끼칩니다. 조선 공학에 쓰이는 다양한 물의 특성은 ITTC(International Towing Tank Conference) Fresh Water and Seawater Properties를 참고하시길 바랍니다.
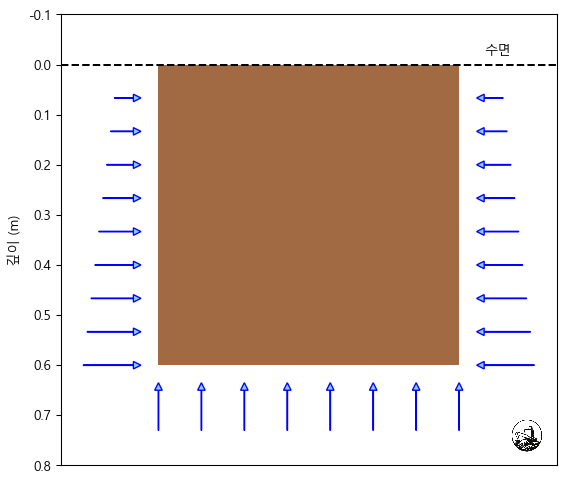
그림 1과 같이 수압은 면적에 수직하게 작용하며 수심이 깊어질 수록 수치가 올라갑니다. 상자의 밑 바닥은 수심이 같으므로 동일한 수압을 받게됩니다.
다른 유체와 마찬가지로 물도 체적탄성계수(bulk modulus of elasticity, \(\mathrm{E_B}\))를 가지고 있으며 이는 잠수함과 같이 수심이 매우 깊은 곳에서는 반드시 고려되어야 합니다. 체적탄성계수는 다음에 기회가 있다면 다른 글에서 다뤄보겠습니다.
2 부력(Buoyancy)
압력이 단위 면적에 수직으로 가해지는 힘이라면 부력은 잠긴 물체를 위로 띄우려는 힘입니다. 중력은 물체를 아래로 당기며 부력을 위로 올리려는 힘이기에 조선 공학에서는 이 두 힘의 균형이 중요합니다. 그림 1을 보면 양 옆에 작용하는 압력는 서로 상쇄가 되나 상자 밑에 작용하는 힘인 부력은 물체를 수면위로 띄우고 있습니다.
많은 분들이 아르키메데스의 원리를 들어보셨을 것입니다.
유체 속에 잠긴 물체는 그 물체가 밀어낸 유체의 무게만큼의 부력을 받는다.
이를 토대로 그림 1 상자에 가해지는 부력을 구해봅시다.
질량 \[ \begin{aligned} F &= P A \\ &= \rho g h \cdot A \\ &= (\rho h A) \cdot g\\ &= m g \\ \end{aligned} \]
중량 \[ \begin{aligned} F &= P A \\ &= \rho g h \cdot A \\ &= (\rho g) \cdot (h \cdot A) \\ &= w V \\ \end{aligned} \]
위에 보이는 부력만큼, 즉 물의 무게만큼 상자가 위의 뜨여지고 있습니다. 많은 분들이 질량으로 힘을 계산하는 방법에 익숙할 것이라 생각됩니다. 중력에 의한 하중인 중량은 유체정역학(hydrostatics)뿐 아니라 유체역학(fluid dynamics)에 전반에 자주 사용되니 유념하여 두기를 바랍니다.
그림 2에 보이는 수심 \(H\ \mathrm{m}\) 밑에 있는 원기둥 모양의 잠수함이 갖는 부력 계산을 해보겠습니다. 잠수함은 반지름 \(R\ \mathrm{m}\)와 길이 \(L\ \mathrm{m}\)를 가지고 있습니다. 앞서 보았던 상자와 마찬가지로 잠수함 양 끝에 작용하는 힘은 같으며 방향은 반대가 되므로 서로 상쇄가 됩니다.
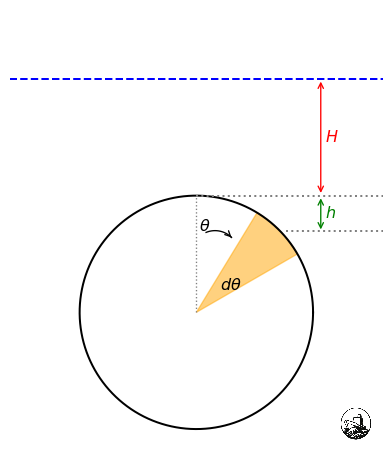
먼저 각도 \(d\theta\)를 가지는 작은 부채꼴 호의 길이와 원기둥 높이를 이용하여 면적을 구하겠습니다.
\[ \begin{aligned} dA &= L \times (R \cdot d\theta) \\ &= LRd\theta \end{aligned} \]
아주 얇고 기다란 면적이 되겠습니다. 하지만 부력은 면적의 수직이 아닌 물체의 위로 향한다는 것을 기억하시나요? 그렇기에 실제 평면면적(flat area) 대신 수면에 투영된 면적(projected area)에 가해지는 압력을 이용하여 부력을 구해줘야 합니다. 이는 위에서 잠수함을 내려다볼때 보이는 면적과 같습니다.
\[ \begin{aligned} dA_{\mathrm{투영}} &= dA \times \cos{\theta} \\ &= (LRd\theta) \cos{\theta} \\ &= LR \cos{\theta} d\theta \\ \end{aligned} \]
그렇다면 수압은 어떨까요? 기본 수심에 미소 면적의 수심까지 더하여 압력을 구할 수 있습니다.
\[ \begin{aligned} P &= \rho g (H+h) \\ &= \rho g [H + (R - R\cos{\theta})] \\ &= \rho g [H + R(1-\cos{\theta})] \\ \end{aligned} \]
이렇게 투영된 미소 면적과 가해지는 압력을 구했으니 미소 면적이 받는 부력을 구해보겠습니다.
\[ \begin{aligned} dF &= P \times dA_{\mathrm{투영}} \\ &= \rho g H [H + R(1-\cos{\theta})] \times LR \cos{\theta} d\theta \\ \end{aligned} \]
이제 적분으로 잠수함 전체에 가해지는 부력을 구해보겠습니다.
\[ \begin{aligned} F &= - \int dP \times dA_{\mathrm{투영}} \\ &= - \int_{0}^{2\pi} \rho g [H + R(1 - \cos{\theta})] \times L R \cos{\theta} d\theta \\ &= - \rho g L R \left\{ \int_{0}^{2\pi} H \cos{\theta}d\theta + \int_{0}^{2\pi} R \cos{\theta} d\theta - \int_{0}^{2\pi} R \cos{\theta} d\theta \right\} \\ &= - \rho g L R \left\{ [-H \sin{\theta}]_{0}^{2\pi} + [-R \sin{\theta}]_{0}^{2\pi} - [R(\frac{\theta}{2} - \frac{\sin{2\theta}}{4})]_{0}^{2\pi}\right\} \\ &= - \rho g L R \left\{ [-H \cancelto{0}{\sin{\theta}}]_{0}^{2\pi} + [-R \cancelto{0}{\sin{\theta}}]_{0}^{2\pi} - [R(\frac{\theta}{2} - \cancelto{0}{\frac{\sin{2\theta}}{4}})]_{0}^{2\pi}\right\} \\ &= \rho g L R^2 \left[ \frac{2\pi}{2} - \frac{0}{2}\right] \\ &= (\rho g) \cdot (L R^2 \pi) \\ &= w V \\ \end{aligned} \]
이렇게 앞서 보았던 부력을 구하는 공식을 다시 볼 수 있었습니다. 하지만 여기서 다음과 같이 몇 가지의 의문점이 생길 수 있습니다.
- 왜 식의 앞에 음수 부호(-)가 붙는가?
- 부력은 유체에 따라 달라질 수 있는가?
- 수심(H)은 자연스럽게 사라지므로 수심에 관계없이 부력은 일정한가?
한번 천천히 생각을 해보고 답해볼 수 있으면 좋겠습니다.
- 유체역학에서 압력에 의한 힘과 면적의 방향성에 이해하여야 합니다. 압력은 바깥쪽에서 안쪽 방향을 가지고 면적은 표면에서 밖을 항하는 법선 방향을 가지고 있습니다. \[d\overrightarrow{F} = -\int P d\overrightarrow{A}\]
- 유체의 밀도에 따라 부력은 달라질 수 있습니다. 대표적인 예시로는 높은 소금 농도로 인하여 보통 바다보다 높은 밀도를 가지고 있는 사해는 사람들이 쉽게 뜹니다.
- 일반적인 상황에서 수심은 부력에 영향을 주지 않습니다. 다만 수심이 깊어질 수록 물의 농도가 바뀌기에 잠수함같이 깊은 수심에서 운행하는 경우에는 변하는 부력을 고려해야 합니다.
물체의 무게와 부력을 안다면 물체가 물에 뜰 수 있을지 없을지 간단히 확인할 수 있습니다. 조선 공학에서는 단순한 선박의 무게와 부력뿐만 아니라 선박의 무게중심, 무게중심의 이동, 외부에서 가해지는 힘 등을 고려하여 선박의 복원성(stability)을 판단해야 합니다. 이에 대하여 다음 글들을 통해 천천히 알아보도록 하겠습니다.
오류나 궁금한 점이 있다면 아래 댓글로 자유롭게 남겨주세요.